F - Games on DAG Editorial /

Time Limit: 5 sec / Memory Limit: 256 MB

配点 : 1600 点

問題文

N 頂点 M 辺の有向グラフ G があります。 頂点には 1 から N まで番号が振られています。 辺には 1 から M まで番号が振られています。 辺 i は頂点 x_i から y_i へ張られています。 ただし、x_i < y_i です。 また、多重辺はありません。

G の M 本の辺集合からある部分集合を選び、G からそれらの辺を取り除いてグラフ G' を作ることを考えます。 このとき、グラフ G' は 2^M 通りあり得ます。

グラフ G' の上で、高橋君と青木君が次のようなゲームで勝負します。 まず、頂点 1, 2 に駒をひとつずつ置きます。 高橋君から始め、高橋君と青木君が交互に次の操作を行います。

  • 頂点 x_i に駒が置かれているような辺 i を選び、頂点 x_i の駒 (2 つある場合は一方のみ) を頂点 y_i へ移動する。 2 つの駒が同一の頂点に置かれてもよい。

先に操作を行えなくなった方が負けです。 二人は最適に行動するとします。

2^M 通りの G' のうち、高橋君が勝つような G' は何通りでしょうか？ 10^9+7 で割った余りを求めてください。

制約

  • 2 ≤ N ≤ 15
  • 1 ≤ M ≤ N(N-1)/2
  • 1 ≤ x_i < y_i ≤ N
  • (x_i,\ y_i) はすべて相異なる。

入力

入力は以下の形式で標準入力から与えられる。

N M
x_1 y_1
x_2 y_2
:
x_M y_M

出力

高橋君が勝つような G' は何通りか？ 10^9+7 で割った余りを出力せよ。

入力例 1

2 1
1 2

出力例 1

1

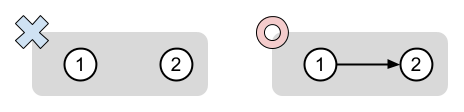
G' は次図の 2 通りです。 高橋君が勝つ場合は ○ で、負ける場合は × で表しています。

b250f23c38d0f5ec2204bd714e7c1516.png

入力例 2

3 3
1 2
1 3
2 3

出力例 2

6

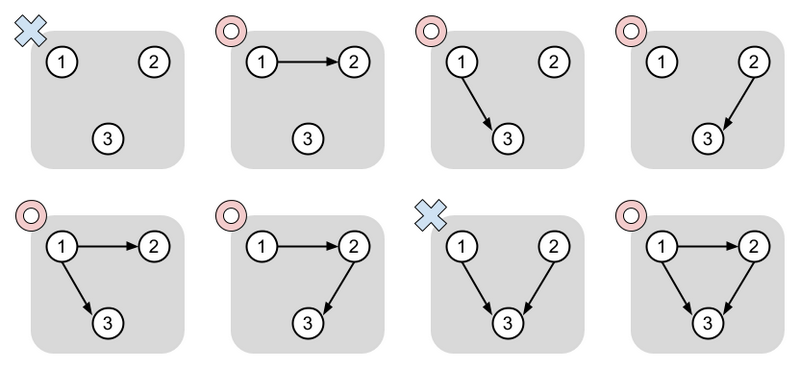
G' は次図の 8 通りです。

8192fd32f894f708c5e4a60dcdea9d35.png

入力例 3

4 2
1 3
2 4

出力例 3

2

入力例 4

5 10
2 4
3 4
2 5
2 3
1 2
3 5
1 3
1 5
4 5
1 4

出力例 4

816

Score : 1600 points

Problem Statement

There is a directed graph G with N vertices and M edges. The vertices are numbered 1 through N, and the edges are numbered 1 through M. Edge i is directed from x_i to y_i. Here, x_i < y_i holds. Also, there are no multiple edges in G.

Consider selecting a subset of the set of the M edges in G, and removing these edges from G to obtain another graph G'. There are 2^M different possible graphs as G'.

Alice and Bob play against each other in the following game played on G'. First, place two pieces on vertices 1 and 2, one on each. Then, starting from Alice, Alice and Bob alternately perform the following operation:

  • Select an edge i such that there is a piece placed on vertex x_i, and move the piece to vertex y_i (if there are two pieces on vertex x_i, only move one). The two pieces are allowed to be placed on the same vertex.

The player loses when he/she becomes unable to perform the operation. We assume that both players play optimally.

Among the 2^M different possible graphs as G', how many lead to Alice's victory? Find the count modulo 10^9+7.

Constraints

  • 2 ≤ N ≤ 15
  • 1 ≤ M ≤ N(N-1)/2
  • 1 ≤ x_i < y_i ≤ N
  • All (x_i,\ y_i) are distinct.

Input

Input is given from Standard Input in the following format:

N M
x_1 y_1
x_2 y_2
:
x_M y_M

Output

Print the number of G' that lead to Alice's victory, modulo 10^9+7.

Sample Input 1

2 1
1 2

Sample Output 1

1

The figure below shows the two possible graphs as G'. A graph marked with ○ leads to Alice's victory, and a graph marked with × leads to Bob's victory.

b250f23c38d0f5ec2204bd714e7c1516.png

Sample Input 2

3 3
1 2
1 3
2 3

Sample Output 2

6

The figure below shows the eight possible graphs as G'.

8192fd32f894f708c5e4a60dcdea9d35.png

Sample Input 3

4 2
1 3
2 4

Sample Output 3

2

Sample Input 4

5 10
2 4
3 4
2 5
2 3
1 2
3 5
1 3
1 5
4 5
1 4

Sample Output 4

816